1 Dada la función
Calcular los valores de los parámetros a y b para que la función ?(?) sea continua y derivable en ℝ. Dar las expresiones de la función ?(?) y de su derivada ?′(?).
Categoría: Funciones
1 Dadas las funciones: y
a) Esboce el gráfico del recinto limitado por las funciones f(x) y g(x).
b) Determinar el área del recinto limitado por las funciones f(x) y g(x).
1 Dada la función ,donde ? y ? son dos parámetros con valores reales.
a) Calcular el valor de los parámetros ? y ? que verifican ?(−2) = 2 y que ?(?) sea continua en ℝ − {5}. Escribir la función resultante ?(?) y calcular su derivada ?′(?).
b) Hallar las ecuaciones de las asíntotas de la función ?(?) si los parámetros toman los valores ? = −1 y ? = −3.
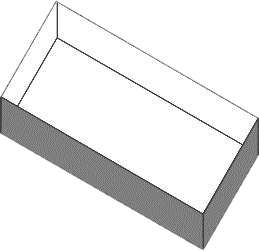
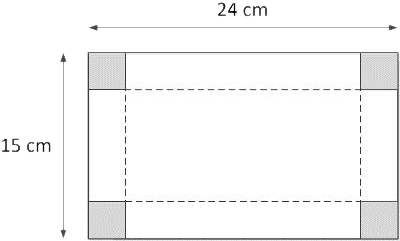
1 Se desea construir una caja sin tapa superior. Para ello, se usa una lámina de cartón de 15 cm de ancho por 24 cm de largo, doblándola convenientemente después de recortar un cuadrado de iguales dimensiones en cada una de sus esquinas. Se determina como requisito que la caja a construir contenga el mayor volumen posible. Indicar cuáles son las dimensiones de la caja y su volumen máximo.
 |
 |
1 Consideremos la función , donde ln denota el logaritmo neperiano. Resuelva justificadamente los siguientes apartados:
a) Presente el dominio, los intervalos de crecimiento y decrecimiento, así como los posibles extremos relativos de la función f(x).
b) Calcule el valor de la integral: .
1 Sean las funciones: y
.
a) Calcule los valores a, b y c de manera que las gráficas de f(x) y g(x) cumplan las dos
condiciones siguientes:
– Se cortan en el punto P(1, 1).
– En dicho punto coincida la pendiente de las rectas tangentes.
Dar las expresiones de las funciones resultantes.
b) Suponiendo a = b = 1 en f(x), halle las asíntotas de la función:
1 Dada la función
Calcular los valores de a, b y c sabiendo que se cumplen las condiciones siguientes:
– Dos de sus extremos relativos se encuentran en los puntos de abcisa x=0 y x=-2
– La función corta el eje OX en el punto x =1
1 Dada la siguiente expresión de la función f, de la que se desconocen algunos valores:
Calcular los valores de y
para que f sea derivable en todo su dominio.
Escribir la función resultante.
1 Determinar los valores de a y b para que la función
tenga un punto de inflexión en el punto (2,8).
