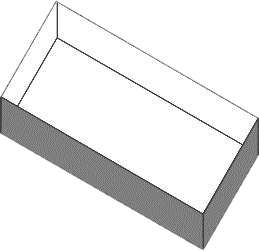
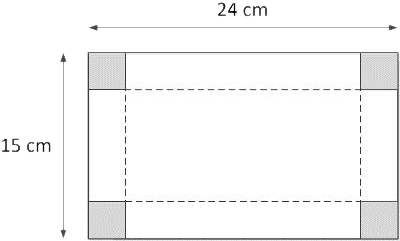
1 Se desea construir una caja sin tapa superior. Para ello, se usa una lámina de cartón de 15 cm de ancho por 24 cm de largo, doblándola convenientemente después de recortar un cuadrado de iguales dimensiones en cada una de sus esquinas. Se determina como requisito que la caja a construir contenga el mayor volumen posible. Indicar cuáles son las dimensiones de la caja y su volumen máximo.
 |
 |
2 Un granjero compra un determinado mes 274€ de pienso para su ganado. Con ese dinero ha comprado un total de 66 sacos de pienso de tres marcas diferentes: A, B y C. Se sabe que el precio de cada marca de pienso que ha comprado es de 5€, 4€ y 4€, respectivamente. También se sabe que el número de sacos adquiridos de la marca C es el doble que el total de sacos comprados de las marcas A y B juntos. Averiguar la cantidad de sacos que el granjero ha comprado de cada una de las tres marcas.
3 Dadas las ecuaciones de los planos:
y
a) Hallar la ecuación de la recta paralela a los planos ?1 y ?2 que pasa por el punto medio del segmento cuyos extremos son ?(1,−1,0) y ?(−1,−3,2)
b) Calcular el ángulo formado por los planos ?1 y ?2.
4 Se ha comprobado que, al aplicar un determinado medicamento, la probabilidad de que elimine el acné a un paciente es del 80 %. Suponiendo independencia de sucesos.
a) Si se lo toman 100 pacientes. ¿Cuál es la probabilidad de que el medicamento actúe con más de 75 pacientes?
b) Si se lo toman 225 pacientes. ¿Cuál es la probabilidad de que el medicamento actúe entre 170 y 190 pacientes?
c) ¿Cuál es el número esperado de pacientes sobre los que NO se eliminará el acné si se toman el medicamento 500 pacientes?
